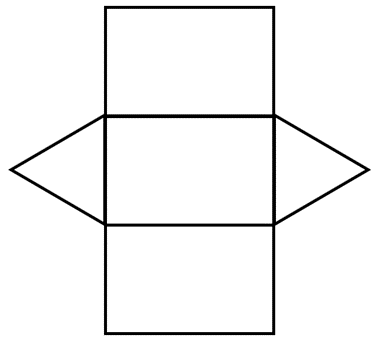
tayatemplates.blogg.se - Triangular prism net

$triangular prism net$

#TRIANGULAR PRISM NET HOW TO#

The surface area of the 3 – dimensional shapes can also be calculated using nets. Each 3 – dimensional shape has its own formula for finding its surface area. The area occupied by a three-dimensional object by its outer surface is called the surface area. Recall that the space occupied by a two-dimensional flat surface is called the area. The surface area of 3 D shapes is similar to the area of 2 D shapes. The surface area of any given object is the area or region occupied by the surface of the object. What is the surface area of 3-dimensional shapes? What is surface area? 3 – dimensional shapes or 3D shapes are the shapes that have all the three dimensions, i.e. One such type of shape is the 3 – dimensional shape. The Sun, the earth and other planets, the mountains and all other things in the world are all of the specific shapes. The alphabets of English shapes are all shapes of different types. We come across many shapes in our daily lives and kids start recognising these shapes even before actually studying about them. The boundary or outline of an object is called its shape. Using nets to find the surface area of a triangular prism.

#TRIANGULAR PRISM NET HOW TO#

How to find the surface area of a triangular prism?.Surface area of a triangular prism using nets.Using nets to find the surface area of a rectangular prism.How to find the surface area of a rectangular prism?.Surface area of a rectangular prism using nets.

Using nets to find the surface area of a cube.

How to find the surface area of a cube?.

How can nets be used to determine surface area?.

Now we don’t have any units for this shape, so we could say that it’s an area of 408 square units because an area should be squared. Adding these numbers together, we get 408. And then we have six times 15, which is 90, and then eight times 15, which is 120, and then 10 times 15, which is 150. So we’ll repeat that process again for the second triangle. One-half times eight times six, well one-half times eight is four, and four times six is 24. So we need to take six times 15 for the pink rectangle, eight times 15 for the green rectangle, and 10 times 15 for the blue rectangle. Now we have the rectangles, and the area of a rectangle is length times width. So we can either take that and multiply by two or write it twice since we have two triangles. And it’s important that we know that that’s a right angle in the corner of the triangle, because that let’s us know that the six is indeed perpendicular. So for the two rectangles, we have one-half times their base of eight times their perpendicular height, which is six. The area of a triangle is one-half times the base times the height. So if we find the area of each of these shapes and we add them together, we will have the surface area. So here we’ve drawn the net of the shape. We have the bottom rectangle, and keep in mind that these are not to scale, and then lastly the blue rectangle. So we have these two triangles, which are our bases we have the pink rectangle, found back here and we have this length as 15, because it matches this one. So our hint tells us to draw the net of this shape, which would be all of the faces laying flat so we can easily see them.

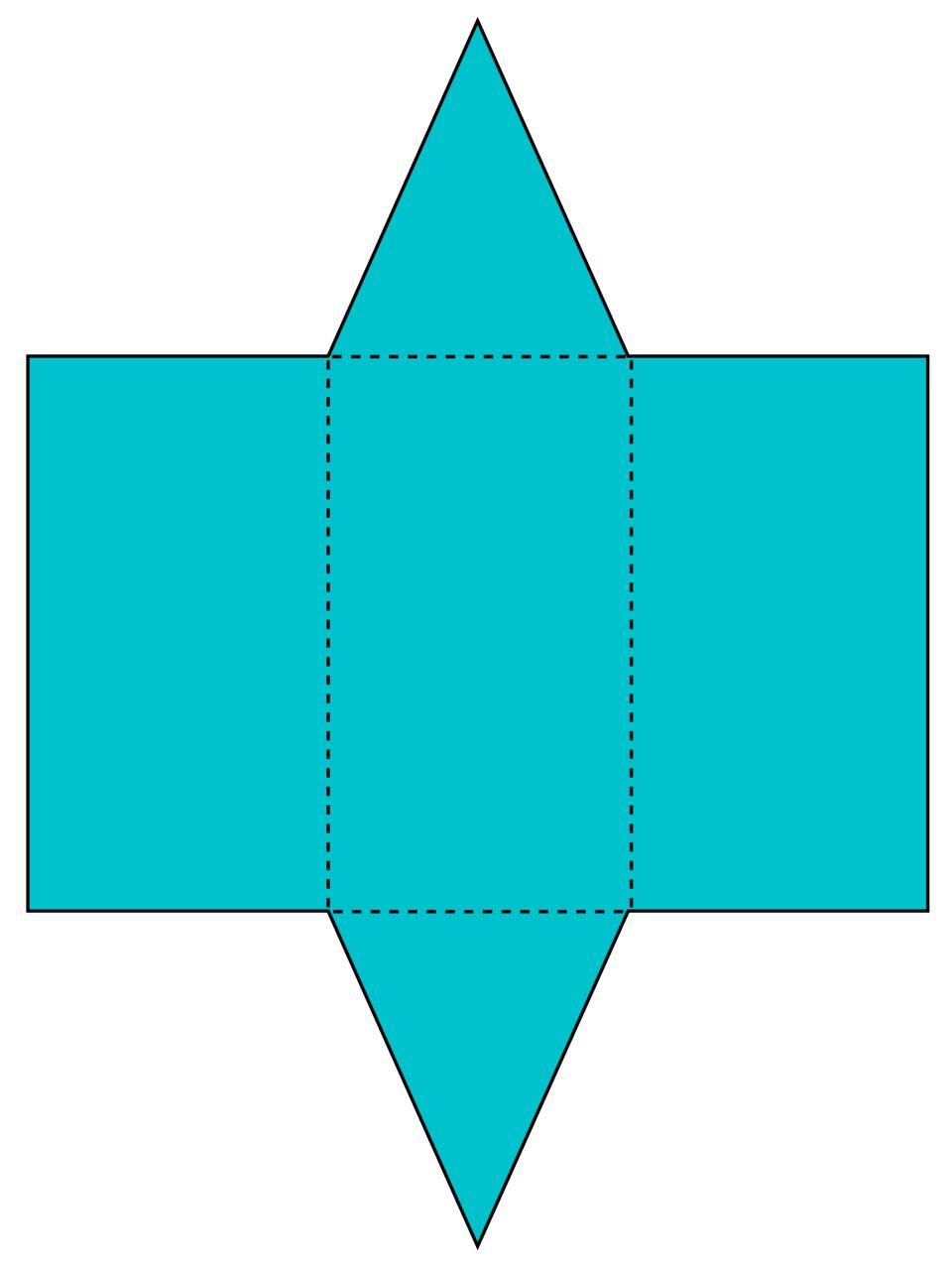
So if we would like the surface area of this shape, we need to add the area of all of the faces together.

That’s what makes up a prism: the two bases and then the rest are rectangles. And it’s a prism because the rest of the faces or the sides is what we can call them are rectangles. The bases, the parallel faces, are triangles. So we have- that this is a triangular prism. Hint: you can draw the net of the shape to help you. Find the surface area of this triangular prism.